I criteri di similitudine (con dimostrazioni)

giugno 20, 2008 a 6:05 PM · Archiviato in Uncategorized

La similitudine è una particolare trasformazione geometrica, contenuta nel piano o nello spazio, che conserva i rapporti tra le distanze.

Ogni similitudine si può ottenere dalla composizione di una omotetia ed una isometria, o viceversa.

Queste trasformazioni mantengono la “forma” dell’oggetto, pur cambiandone la posizione, l’orientazione o la grandezza; quindi due oggetti simili hanno la stessa “forma”.

In termini tecnici, due poligoni sono simili se hanno lo stesso numero di lati, gli angoli corrispondenti congruenti e i lati corrispondenti proporzionali.

La similitudine tra due oggetti si indica con il segno {\sim} (es. {A \sim B} ).

Nella geometria piana particolare rilevanza hanno i tre criteri di similitudine tra triangoli.

Primo criterio di similitudine

Enunciato

Se due triangoli hanno due angoli congruenti, allora sono simili.

Si noti che se due triangoli hanno due angoli congruenti, siccome la somma degli angoli interni è sempre di 180° (tale affermazione deriva direttamente dal V postulato di Euclide) hanno per forza anche il terzo angolo congruente.

Ipotesi

{ \alpha \cong \alpha ' ; \beta \cong \beta ' ; \gamma \cong \gamma ' ; }

Tesi

{\triangle ABC \sim \triangle A'B'C'}

Dimostrazione

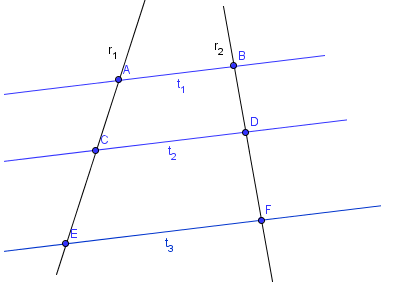
Una volta definito il teorema di Talete, dimostrare il primo criterio di similitudine dei triangoli è estremamente semplice: basta infatti sovrapporre i due triangoli in modo che abbiano un vertice in comune e i lati a coppie paralleli: per il teorema prima citato immediatamente arriveremo alla conclusione che

{AB:A'B'=BC:B'C'=CA:C'A'}

Avendo gli angoli uguali e i lati in proporzionalità diretta, si può dedurre che:

{\boxed{\triangle ABC \sim \triangle A'B'C'}}

WWWWW

Secondo criterio di similitudine

Enunciato

Se due triangoli hanno un angolo congruente e i lati che lo comprendono direttamente proporzionali, allora sono simili.

Ipotesi

{ \alpha \cong \alpha ' }

{\displaystyle{{AB}:{AC}={A'B'}:{A'C'}}}

Tesi

{\triangle ABC \sim \triangle A'B'C'}

Dimostrazione

La dimostrazione è molto simile a quella del primo criterio di similitudine.

Infatti, conseguentemente al teorema di Talete, i due triangoli avranno:

{ \alpha \cong \alpha ' ; \beta \cong \beta ' ; \gamma \cong \gamma ' ; }

proprio perché hanno due lati direttamente proporzionali.

Da qui ci si riallaccia al primo criterio di similitudine e si completa:

{AB:A'B'=BC:B'C'=CA:C'A'}

Avendo gli angoli uguali e i lati in proporzionalità diretta, si può dedurre che:

{\boxed{\triangle ABC \sim \triangle A'B'C'}}

WWWWW

Terzo criterio di similitudine

Enunciato

Se un triangolo ha i tre lati direttamente proporzionali a quelli di un altro triangolo, allora i due triangoli sono simili.

Ipotesi

{\displaystyle{\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{CA}{C'A'}}}

Tesi

{\triangle ABC \sim \triangle A'B'C'}

Dimostrazione

Sempre come conseguenza del teorema di Talete, i due triangoli avranno:

{ \alpha \cong \alpha ' ; \beta \cong \beta ' ; \gamma \cong \gamma ' ; }

Ma visto che, se due poligoni hanno lo stesso numero di lati, gli angoli corrispondenti congruenti e i lati corrispondenti proporzionali, allora:

{\boxed{\triangle ABC \sim \triangle A'B'C'}}

WWWWW

Lascia un commento

Teorema di Talete (con dimostrazione)

giugno 19, 2008 a 5:21 PM · Archiviato in Uncategorized

Uno dei più importanti teoremi della materia è senza alcun dubbio il Teorema di Talete.

Enunciato
Un fascio di rette parallele secante due trasversali determina su di esse classi di segmenti direttamente proporzionali.

Teorema di Talete

Ipotesi

{t_1 \parallel t_2 \parallel t_3}

Tesi

{\displaystyle{\frac{AC}{BD}} = {\frac{CE}{DF}} = {\frac{AE}{BF}}}

Dimostrazione

Dato un triangolo ABC, tagliato da un segmento DE parallelo a BC.

Si congiungano D con C ed E con B, ottenendo due triangoli BDE e CDE.

Tali triangoli sono equivalenti, in quanto hanno la stessa base e stessa altezza (tale altezza sarebbe la distanza tra DE e BC).
Quindi possiamo tranquillamente scrivere:

{A_{BDE} : A_{ADE} = A_{CDE} : A_{ADE}}

Ma, avendo CDE e ADE la stessa altezza (col piede sul lato AC), si può dedurre che il rapporto tra le aree è uguale al rapporto delle basi:

{A_{BDE} : A_{ADE} = BD : DA}

Per la stessa ragione:

{A_{CDE} : A_{ADE} = CE : AE}

Unendo le ultime due proporzioni possiamo così ottenere che:

{\boxed {BD: AD = CE : AE}}

WWWWW

Il primo a dimostrare il teorema di Talete in questo modo fu Euclide nel IV secolo a.C.

Comments (1)

Tutto parte da qui!

giugno 19, 2008 a 4:25 PM · Archiviato in Uncategorized

Sottolineiamo: qui parliamo di Geometria euclidea; prevalentemente piana.

Non voglio dilungarmi tanto sull’introduzione alla geometria euclidea: per questo ci sono molti altri siti che se ne occupano (vi consiglio Wikipedia data la sua semplicità e considerando che è continuamente rivista).

Vi dirò soltanto che la Geometria euclidea sostanzialmente è quella che si studia a scuola e che viene maggiormente utilizzata nelle applicazioni pratiche.

Il postulato da cui prende vita questa geometria è il seguente:

Data una retta e un punto esterno ad essa esiste una e una sola retta parallela alla retta data che passa per tale punto.

Tale fatto ai tempi di Euclide fu chiamato V postulato.

Negando tale postulato si dà origine ad altri tipi di geometrie, che possono essere molto diverse da quella euclidea.

Ma vi sono varie altre formulazioni di tale postulato, tutte equivalenti, per esempio:

  • Si postula che se una retta, incontrante altre due, forma gli angoli interni da una stessa parte minore di due retti, le due rette, prolungate all’infinito, si incontrano dalla parte in cui sono i due angoli minori di due retti.
  • Date due rette parallele tagliate da una trasversale, la somma dei due angoli coniugati interni è pari ad un angolo piatto.
  • In un qualsiasi triangolo la somma degli angoli interni è pari ad un angolo piatto.

Comments (1)